Using anti-aliasing, digital, and arithmetic mean filtering

Filtering techniques for analog inputs explained

Introduction

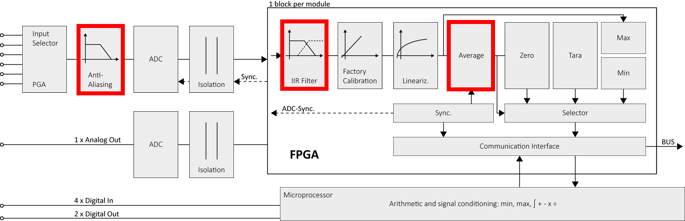
Filtering is a critical aspect in measuring analog signals, serving to enhance the accuracy and reliability of the acquired data. Filtering techniques are applied to selectively allow certain frequencies while attenuating or eliminating others, ensuring that the measured data reflects the true characteristics of the signal of interest. The Q.series measurement modules feature three types of filtering: anti-aliasing filtering, digital filtering, and arithmetic mean filtering.

Anti-aliasing filter

Measurement modules have a fixed sample rate. Ideally, this sample rate should be greater than or equal to 2x the highest frequency component found in the input signal (Nyquist limit). Violating this rule introduces unwanted frequency band signals known as aliasing.

The purpose of the anti-aliasing filter (AAF) is to keep the alias (difference frequency) out of the digitized data. Importantly, the AAF does not affect the module's sampling rate.

For example:

Module sample rate: 100 kS/s
Anti-aliasing filter: 20 kHz

In this scenario, the module always samples at 100 kS/s per channel. The role of the filter is to limit the bandwidth to approximately 20 kHz, not the sampling rate.

Digital filters

After passing through galvanic isolation, the measurement modules offer the option to set digital input filters integrated into the FPGA software. These filters operate in conjunction with the internal frequency of the A/D converter. The IIR filters can be configured as low-pass (LPF), high-pass (HPF), band-pass (BPF), and band-stop (BSF). Additionally, they can be configured as a Bessel or Butterworth filter.

The digital filters are based on an IIR (infinite impulse response) transfer function, also known as a recursive filter, and are executed on the measurement module's FPGA. As the filtering takes place after A/D conversion, its purpose is to eliminate noise introduced during the conversion process. The implementation of the IIR filters was guided by 'The Scientist and Engineer's Guide to Digital Signal Processing'.

The standard digital filters are Chebyshev Type I filters, allowing ripple only in the passband. They include the following types:

4th order low-pass filter
4th order high-pass filter
4th order band-pass filter

The filters are implemented using integer variables, and the intermediate results are currently up to 72 bits wide. The filter frequency ratio is possible up to 1/1,000,000. For example, a measurement module with a 100 kS/s ADC sample rate supports a cut-off frequency as low as 0.1 Hz. The available frequency ratios are defined in the tables below. The filter ratio is calculated as the cut-off frequency divided by the sample rate.

Low-pass filter cut-off frequencies

Frequency ratio	100 kS/s	25 kS/s	20 kS/s	10 kS/s
0.000005			0.1
0.000008		0.2
0.00001	1		0.2	0.1
0.00002	2	0.5		0.2
0.000025			0.5
0.00004		1
0.00005	5		1	0.5
0.00008		2
0.0001	10		2	1
0.0002	20	5		2
0.00025			5
0.0004		10
0.0005	50		10	5
0.0008		20
0.001	100		20	10
0.00175			35
0.002	200	50		20
0.0025			50
0.004		100
0.005	500		100	50
0.008		200
0.01	1000		200	100
0.02	2000	500		200
0.025			500
0.04		1000
0.05	5000		1000	500
0.1	10000		2000	1000

High-pass filter cut-off frequencies

Frequency ratio	100 kS/s	25 kS/s	20 kS/s	10 kS/s
0.0000001	0.1			0.01
0.000004		0.1
0.000005			0.1
0.00001	1			0.1
0.00004		1
0.00005			1
0.0001	10			1
0.0004		10
0.0005			10
0.001	100			10
0.004		100
0.005			100
0.01	100			100
0.02	2000	500
0.03	3000
0.04		1000
0.05	5000		1000	500

Band-pass filter cut-off frequencies

The available cut-off frequencies for the band-pass filter are a combination of the low-pass and high-pass cut-off frequencies.

Arithmetic mean filter

Arithmetic mean filtering is carried out in the module after signal conditioning, which includes digital filtering, linearization, and scaling. This filter computes the mean average of a set of samples between two syncs of the controller. For instance, if the bus update rate is set to 1 kHz, and the module has a sample rate of 20 kS/s, a maximum of 20 samples can be averaged in the module. However, if the bus update rate is also set to 20 kHz, no averaging occurs in the module. If no arithmetic mean filtering is applied in the module, and the bus update rate is set to 1 kHz, the controller will receive every 20th value from the module.

There are two possibilities for configuring the sample size for the arithmetic mean filter:

Manual sample count
This parameter defines the sample size for calculating the mean average. The sample count is related to the ADC sample rate and determines the update rate of the measurement value (ADC sample rate/sample count = update rate). For instance, a module with an ADC rate of 20 kS/s and a sample count of 100 will result in a maximum possible controller update rate of 200 Hz.
Automatic sample count

When the sample count parameter is set to 0, the optimal sample size is automatically determined by dividing the ADC sample rate by the bus sample rate. For example, a module with an ADC sample rate of 100 kS/s and a bus sample rate of 1 kS/s will result in a sample size of 100.

The automatic sample size setting is not available for the A117 module that is installed in the Q.monixx.

The automatic sample count option only works when the ADC is synchronized to the bus (LocalBus or EtherCAT only).